Camp gravitatori
Test bàsic 

Preguntes sobre coneixements bàsics d'aquest tema. S'obtendrà una nota sobre 10 punts. Les respostes incorrectes descompten puntuació.
Força d'atracció gravitatòria 


Isaac Newton publicà la llei de la gravitació universal el 5 de juliol de 1687. Amb aquesta llei aconseguí explicar les lleis de Kepler del moviment planetari.

• L'expressió de la llei de gravitació universal,
• La constant de gravitació universal, almenys amb el valor aproximat a G = 6.67 10-11 N |m2 kg-2.
• Calcular la força d'atracció entre masses.
• Que el valor aproximat de la gravetat a la superfície terrestre és g = 9.80 m/s2.
1
A quina distància del centre de la Terra la gravetat és la meitat de l'acceleració de la gravetat en superfície?
RT = 6370 km.
2
Quina és la força d'atracció gravitatòria de la Terra sobre la Lluna quan es troben a la distància mitjana de l'òrbita, 384400 km? Determina el resultat en zettanewtons
(1 ZN = 1021 N)
MT = 5.972 1024 kg, ML = 7.349 1022 kg.
3
Quina és la força d'atracció gravitatòria del Sol sobre la Terra?
MS = 1,9891 1030 kg, MT = 5.972 1024 kg, distància mitjana Sol-Terra = 149,6 106 km.
4
Quantes vegades més gran és l'atracció gravitatòria del Sol sobre la Terra que l'atracció de la Lluna sobre la Terra?
MS = 1,9891 1030 kg, MT = 5.972 1024 kg, ML = 7.349 1022 kg, distància mitjana Sol-Terra = 149,6 106 km, distància mitjana Terra-Lluna = 384400 km.
Gravetat a la superfície d'un planeta 


Els planetes no són perfectament esfèrics ni tenen la massa distribuïda de manera uniforme, però suposar-ho permet obtenir una estimació de l'acceleració de la gravetat amb la llei de gravitació universal.

• Calcular l’acceleració de la gravetat a la superfície d’un planeta a partir de la llei de gravitació.
5
Quina és l'estimació per a l'acceleració de la gravetat a la superfície de la Terra que dona la llei de gravitació universal? Determina la resposta arrodonida a les centèsimes.
MT = 5.972 1024 kg, RT = 6370 km.
6
Calcula l'estimació de la gravetat a la superfície de Mart a partir de la massa del planeta, 6.417 1023 kg, i el radi, 3396 km. Determina la resposta amb dos decimals.
7
Un planeta hipotètic amb la mateixa gravetat superficial que la Terra, té un radi 1.5 vegades més gran. A quantes terres és igual la massa d'aquest planeta?
Intensitat del camp gravitatori 


El camp gravitatori en el que es mouen els satèl·lits de Júpiter està dominat per les masses del Sol i de Júpiter mateix. El camps s'han de sumar vectorialment. Considerar la suma de dos camps, és el cas més senzill que es pot tractar.

• Calcular el camp gravitatori creat per dues masses en un punt d'un pla que les conté.
(Va molt bé saber identificar gràficament la direcció i el sentit del camp resultant abans de resoldre el problema numèricament.)
8

En un pas de la Lluna pel perigeu, el centre de la Lluna està a d = 359503 km del centre de la Terra. A quina distància de la Lluna es troba el punt intermedi on l'atracció gravitatòria de la Lluna just supera l'atracció de la Terra? Determina el resultat arrodonit a km.
MT = 5.972 1024 kg, ML = 7.349 1022 kg.

9
Per resoldre el problema 8 es planteja una equació que té dues arrels. Una arrel és la solució demanada en el problema. Raona quin és el significat de l'altra arrel. Quina és la intensitat del camp gravitatori degut a la Terra i a la Lluna associat a la segona arrel?
MT = 5.972 1024 kg, ML = 7.349 1022 kg.
10
Què val la component x del camp gravitatori d'una esfera de 2.49 1020 kg en un punt a 400 km del centre en la direcció de latitud 30º com mostra la figura?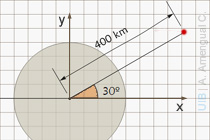
11
Una estrella S amb la mateixa massa del Sol té un sistema planetari. Què val la intensitat del camp gravitatori degut a l'estrella S i un dels seus planetes, J, a la posició d'un altre planeta P quan aquest està en quadratura amb J com mostra la figura?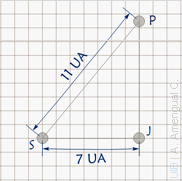
1 UA = 149.6 109 m, MS = 2 1030 kg, MJ = 0.2 1030 kg
12
Quina és la intensitat del camp gravitatori en un punt que equidista 700 km de dues esferes de 5.2 1020 kg com mostra la figura?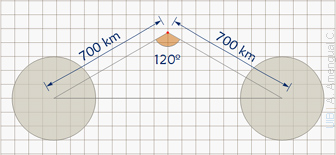
Potencial gravitatori i energia 



• Conèixer que el camp gravitatori és central i, per tant, conservatiu.
• Conèixer la funció potencial gravitatori i saber calcular el seu valor (la funció potencial es definirà perquè valgui zero a l'infinit si no s'indica un altre origen en l'enunciat).
• Saber calcular l'energia.
• Saber que a una altura h, prop de la superfície d'un planeta, l'energia potencial gravitatòria s'aproxima per m g h.
13
Què val el potencial gravitatori en el punt on s'ha demanat el camp a l'exercici 12?
14
Quina és l'energia potencial gravitatòria a la Lluna d'una massa de 5 kg a 100 metres d'altura? Fes el càlcul de dues maneres:
i) Ep = m g h (l'acceleració de la gravetat g a la superfície de la Lluna s'ha de calcular a partir de la massa ML = 7.349 1022 kg i el radi RL = 1737 km);
ii) Ep = m (/V|(RL + h) − /V|(RL)).
Comprova que els dos valors difereixen en dècimes de joule.
15
En la línia entre els centres de la Terra i la Lluna, hi ha un punt on el camp gravitatori de la Terra i de la Lluna s'anul·la. Què val el potencial gravitatori en aquest punt quan els centres estan a 359503 km?

 Temes
Temes  Portada
Portada  Olimpíada
Olimpíada 

